Example to calculate short circuit current for circuit breaker
The purpose of this write-up is to help the reader estimate the example before you hire the PE to do the official calculation.
All electrical systems are susceptible to short circuits. The short circuit currents can produce considerable thermal and mechanical stresses in electrical distribution equipment. Therefore, it’s important to protect personnel and equipment by calculating short-circuit currents during system upgrade and design. Since these calculations are life-safety related, they’re mandated by 110.9 of the NEC.
In the example shown in Fig. 1, our goal is to find the irrupt rating for the two breakers (1600A and 250A), and also find the withstand rating of the two panels (main and sub-panel).
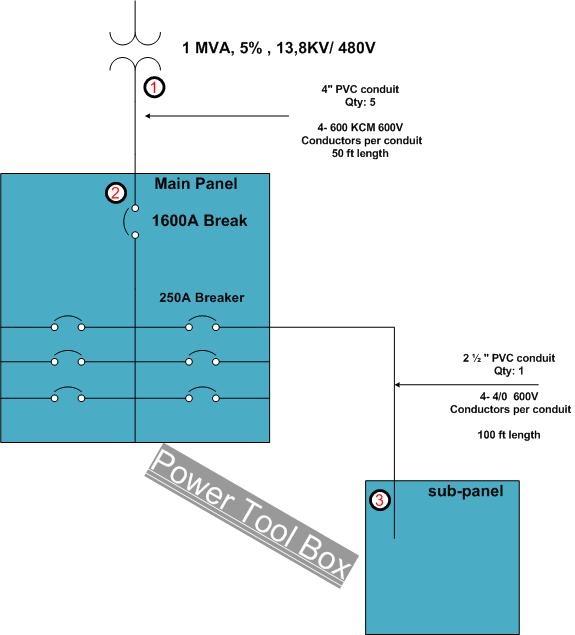
I F.L = P / (1.73 * V L-L ); where P is the transformer power rating in VA, and V L-L is the line to line RMS voltage at the secondary side of the transformer.
I F.L = 1,000,000/ 1.73*480 = 1,202 A; the I F.L is the full load current of the transformer.
Now, to find the short circuit rating of point 1 (i.e. if we bolt all the three wires of the secondary side of the transformer, and how much current we will see at that point):
I S.C. for 3 Ph = I F.L /Z%; where I.S.C. is the short circuit current, and Z% is the transformer impedance; which usually can be obtained from the local utility company.
I S.C. 3 ph for point 1 = 1202 /0.05 = 24,506 A or 24.5 KA (this is the available short circuit current at point 1).
The short circuit current at point 2 will be lower than point 1, due to the line impedance (line impedance for the cables will impose the current).
The calculation below will show the short circuit current at point 2:
From the drawing; cable length = L = 50 ft.
F = (1.73 * L* I S.C. 3 ph) / (C *n*V L-L); F for the three-phase fault ——– [1]
F = (2 * L* I S.C. L-L) / (C *n*V L-L); F for line to line fault ——– [2]
F = (2 * L* I S.C. L-N) / (C *n*V L-N); F for Line to Neutral fault ——–[3]
In our case, we will use equation #1 for this example.
C = the conductor factor; the value can be obtained from the table (1) by locating the conductor’s size in the proper configuration
n = the number of parallel runs
L = length in ft.
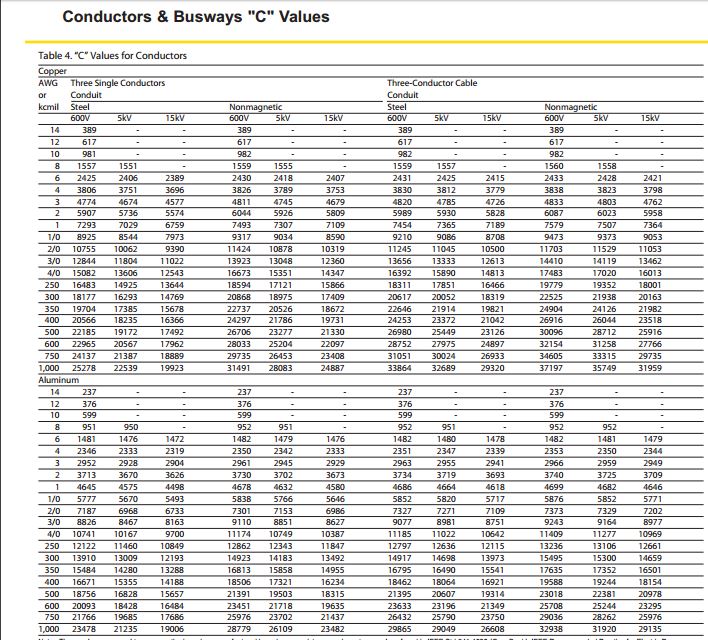
| Table (1): These values are equal to one over the impedance per foot, based upon resistance and reactance, found in IEEE std. 241 |
F = (1.73 *50 *24,506) / (28,303*5*480) = 0.031206
M = 1/(1+F) = 0.969738; where M is the multiplier
I S.C. 3 ph for point 2 = 24506* M = 24506*0.969738 = 23,764 A or 23.7 KA (this is the available short circuit current at point 2)
It’s worth mentioning that the further the main panel is from the transformer, the lower the short circuit current, but you will have a bigger voltage drop, due to the larger line impedance.
The calculation below will show the short circuit current at point 3 (this is similar to the point 2 calculation):
F = (1.73 * L* I S.C. 3 ph at point 2 ) / (C *n*V L-L)
F = (1.73 *100*23,764) / (16673*1*480) = 0.51370
M = 1/(1+F) = 1/1.51370 = 0.6606
I S.C 3 ph for point 3 = 23,764 *0.6606 = 15,699 A or 15.7 KA
I hope you find this example and the short circuit calculation useful. Please let me know if you have any questions.

